巧用弹簧类比解决L-C谐振电路
前言
我相信很多同学在做涉及L-C谐振电路时都会遇到这样一种情况。把振荡频率记下来,但是时间一长又忘记了。或者题目换一种问法以及问一些其他的物理量的变化方式就又不会做了。
其实想要理解L—C谐振电路很简单,你只要把它和弹簧振子进行类比就可以了。
我们知道弹簧振子在振动过程中,小球的动能和整体的弹性势能总和是不变的。其实在谐振电路中也是一样的,电感存储的磁能和电容器存储的电能总和也是不变的。因此,完全可以把弹簧阵子和LC谐振电路类比着一块去学。不过在此之前,我们先来看一下电容器存储的电能和电感存储的磁能。
电容器存储电能的公式
我们知道电容器存储的电荷量与电容器两端的电压满足关系, 表示电容器电荷量, 表示电容器两端电压。现在来讨论一下电容器的存储的电能公式。根据 的关系画出电容器的 图像如图 1所示
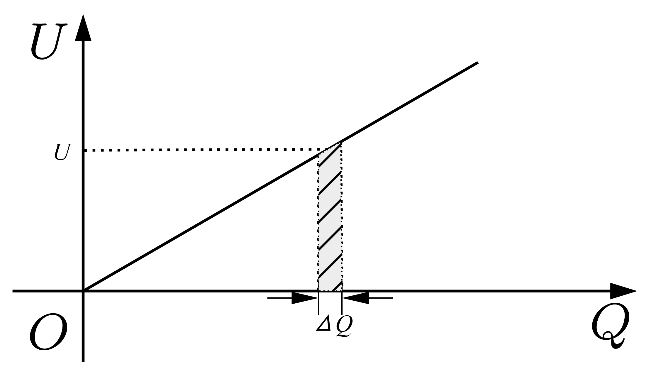
图1
当电容两端电压为时,若有的电荷量从电容器的一端流到了另一端,则在这个过程中电荷量对应的电势能减少了,电荷量的减少会使电容器两端电压发生变化,但是这里电荷量减少的非常小,也就是说是一个小量,这样的话电压可以近似认为不变。因此图像中阴影部分的面积近似表示电荷量改变电容器释放的电荷量。也就是说图像围成的面积表示释放的电能(也可认为存储的电能)。
这样当电容器存储的总电荷量全部释放完毕时,释放的电能为。于是我们得到了电容器的储能公式
对于电容器,电容器的电能不发生突变,因此电容器的电压是不会发生突变的。
电感器存储磁能公式
当线圈通过一个变化的电流时,线圈内部的磁场将会产生变化,线圈的磁通量发生改变,根据楞次定律,线圈将产生感应电动势,这个感应电动势的存在阻碍电流的变化。由法拉第电磁感应定律,感应电动势的大小满足,对于一个线圈,线圈内部的磁通量与线圈的电流成正比,因此线圈产生的感生电动势大小可以写成
其中是电感线圈产生的电动势也是自感线圈两端的电压,我们将上式变换一下,将同乘左右两边有。
这个公式的左边它表示什么物理含义呢?我们现在就来看一下。它表示的是在时间内存储的电能或者是消耗的电能。这些能量都来源于磁能,或者都以磁能的形式进行存储。总的来说,这个式子就表示在时间内电感原件存储的磁能。
那么接下来我们就需要进行累加。将整个过程中的能量累加起来。在这里我们用图像进行累加,另,画出的图像,如图2所示

图2:Y与I的函数关系式
在图 2中,假设某时刻电感的电流为 ,经过一段非常微小的时间,在这段小时间间隔内电流变化为,那么这段时间间隔内电感增加的能量为,当时间间隔取的足够小时,阴影部分的面积就可以看成,因此根据公式所表达的含义,可以得出围成的面积表示电感的储能。于是得到电感的储能公式
由上式可知,当电感线圈电流为 ,电流逐渐减少为0时,电感释放的能量为 。在电感中当电流变化时产生感应电动势,线圈将电能转化成磁能存储起来,当电流发生减少时磁能通过电磁感应将磁能转化为电能阻碍电流的减少。
对于电感,由于能量不可能突变,因此电感线圈中的电流不发生突变。
L-C谐振电路中的能量转换
当电感与电容串联就形成了一个LC电路,不考虑电路中任何能量损失。整个电路中只有电感存储的磁能与电容器存储的电能来回转化。于是得到
例如,如果一个充满电的电容器(假设充满电后电容器电压为),与一个电感串联。刚开始时状态如图3所示,随后电容器放电,存储的电能逐渐减少,电容器两端电压逐渐变小,减少的电能转化成电感的磁能,根据电感磁能公式可得电感上的电流逐渐变大电流方向为逆时针;当电容器电能全部转化成电感的磁能时电容器两端电压为0,这个时候电流最大电感中的磁能最大,如图4所示的状态。
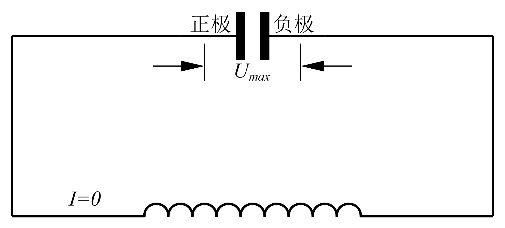
图3:电容刚开始放电

图4:正向电流最大
随后电容器被反向充电,电流方向依旧为逆时针,电容器的右极板为正极,电容器两端电压方向与初始状态相反,电感对电容充电,电感的磁能逐渐转化成电容器的电能,当电流为0时电感的磁能全部转化成电容的电能。这个时候电容器两端电压再次达到初始值只不过电压方向与初始状态相反,其状态如图5所示;随后电容器反向放电,电流方向为顺时针,电容器的电能逐渐转化成磁能,电流逐渐增大,当电流最大时电容器两端电压为0,电能全部转化成磁能,如图6所示。
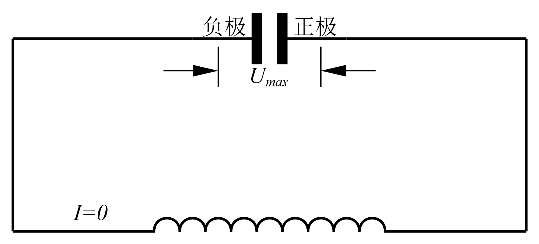
图5:电容反向电压最大

图6:反向电流最大
随后电流减小为0时,电容器两端电压最大,再次达到了其状态与初态相同。这就是LC谐振电路的一个循环。后面发生周期性变化过程重复上述过程。
LC谐振电路与弹簧振子之间的类比关系
仔细分析上面电容电能和电感磁能的变化情况,我们发现其变化规律与弹簧谐振子中动能与势能的变化一摸一样。这就提示我们将LC谐振电路与弹簧谐振子进行横向比较,学习。 在弹簧谐振子中,物体的动能与弹性势能的总和保持不变,即有
根据速度的定义又可以写成,于是上式子可以重新写成
在LC谐振电路中有
根据以及电流的定义上式可以重新写成
看到了吗?我们把弹簧振子系统能量的公式拿过来两者对比一下
现在应该注意到了吧,在能量上弹簧振子与LC谐振电路满足相同的公式。也就是在学习时,完全可以将两者类比学习
也就是说LC谐振电路中电容器的电荷量类比成弹簧谐振子中的位移 ;LC谐振电路中电流类比成弹簧谐振子中的速度 ;谐振子中物体的质量 类比成电感 ,电容的倒数 类比成劲度系数 。
谐振电路各状态和弹簧谐振子各状态的对比图分别如下图7所示


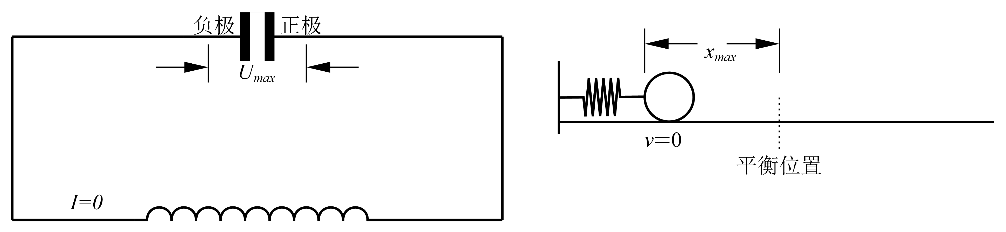

对于弹簧谐振子振动周期为
根据上面的类比关系可以得到LC谐振电路中的振荡周期
结语
在物理学习的过程中,如果两个系统有相同的数学公式、方程。那么这两类系统完全可以类比着去学习。
以后在遇到LC谐振电路时只要将其类比成弹簧谐振子用我们熟悉的系统去类比学习就行